Non-Orthogonal Configuration Interaction (NOCI)"

Processes relevant to photocatalysis and multiple exciton generation are strongly correlated with the strength of the electronic coupling between initial and final states. Many theoretical studies rely on phenomenological models and only consider the highest occupied and lowest unoccupied orbitals of the interacting molecules. There are of course also many studies based on density functional theory and in many cases these approaches are very successful in describing the main features of the interaction. However, there are systems that call for complementary information based on multiconfigurational approaches. 

The use of one set of orthogonal orbitals to describe all the states of the system tremendously simplifies the computation of the electronic structure and is therefore the method of choice in almost all cases. However, this approach has some disadvantages that we try to overcome in our implementation of non-orthogonal CI (NOCI) in the computer code GronOR. To illustrate the disadvantage of an orthogonal orbital approach we focus on the following two schematic representation of charge transfer and energy transfer from A to B

charge transfer: A + B → A⁺ + B^-

energy transfer: A* + B → A + B*

where A and B stand for the ground states of the two fragments, A* and B* for local excited states and A+ and B- for the cationic and anionic states. It is readily seen that the optimal orbitals of all these states can be quite different from each other, especially for the charged molecules. This orbital relaxation can only be treated approximately in an orthogonal orbital approach, but is obviously fully accounted for when one allows for different orbitals for different states. The drawback is that orbitals are no longer orthogonal and the calculation of matrix elements becomes much more complicated. 

Based on the General Non-Orthogonal Matrix Elements (GNOME) algorithm, the NOCI-Fragments method has been very efficient implemented in the massively parallel and GPU accelerated GronOR code. The method counts with the following steps: First, calculation of the fragment wave functions with any (multiconfigurational) wave function that best suits the problem. In the examples listed above, six different wave functions should be calculated; the ground states A and B, the excited states A* and B* and the A+ and B- wave functions. These calculations can either be done on isolated fragments, or even better, on a fragment embedded in a (frozen) embedding. In the second step the so-called multi-electron basis functions (MEBFs) are constructed as antisymmetrized spin-adapted products of the fragment wave functions calculated in step 1. Here, we need the AB, A*B AB* and A+B- MEBFs, which describes the ground state of the AB dimer, a local excited state on A, a local excited state on B and the charge transfer state, respectively. The third and computationally most intensive step concerns the calculation of the matrix elements between the MEBFs. Although there are only few matrix elements to be calculated (10 in this example), each matrix elements counts with a huge number of contributions. Let's assume that the ground state of A and B are both described by a multiconfigurational wave function of 20 determinants, which is actually very small. The MEBF AB is then a linear combination of 400 determinants, and the matrix element < AB ' H ' AB > has 160 000 non-zero contributions. The final step is about the interpretation of the results. The matrix elements give a measure of the probability of a process to happen, for example if < AB* ' H ' A*B > turns out to be very large, an energy transfer from A to B is likely to happen. Furthermore, the eigenvectors of the Hamiltonian --the NOCI wave function-- give a direct interpretation of the electronic structure in chemically intuitive concepts as charge transfer, local excited states and any other diabatic functions that were included in the NOCI.

At present we are working on the elucidation of multi exciton generation (illustrated in figure 1) in perylenediimides and indolonaphtyridine derivatives. We focus on the coupling between the S0S1 and T1T1 states and the importance of the charge transfer states in the singlet fission process. Futhermore, we are developing new application of the NOCI methods in the field of phtocatalysis and the determination of non-adiabatic couplings for the simulation of excited state dynamics. 

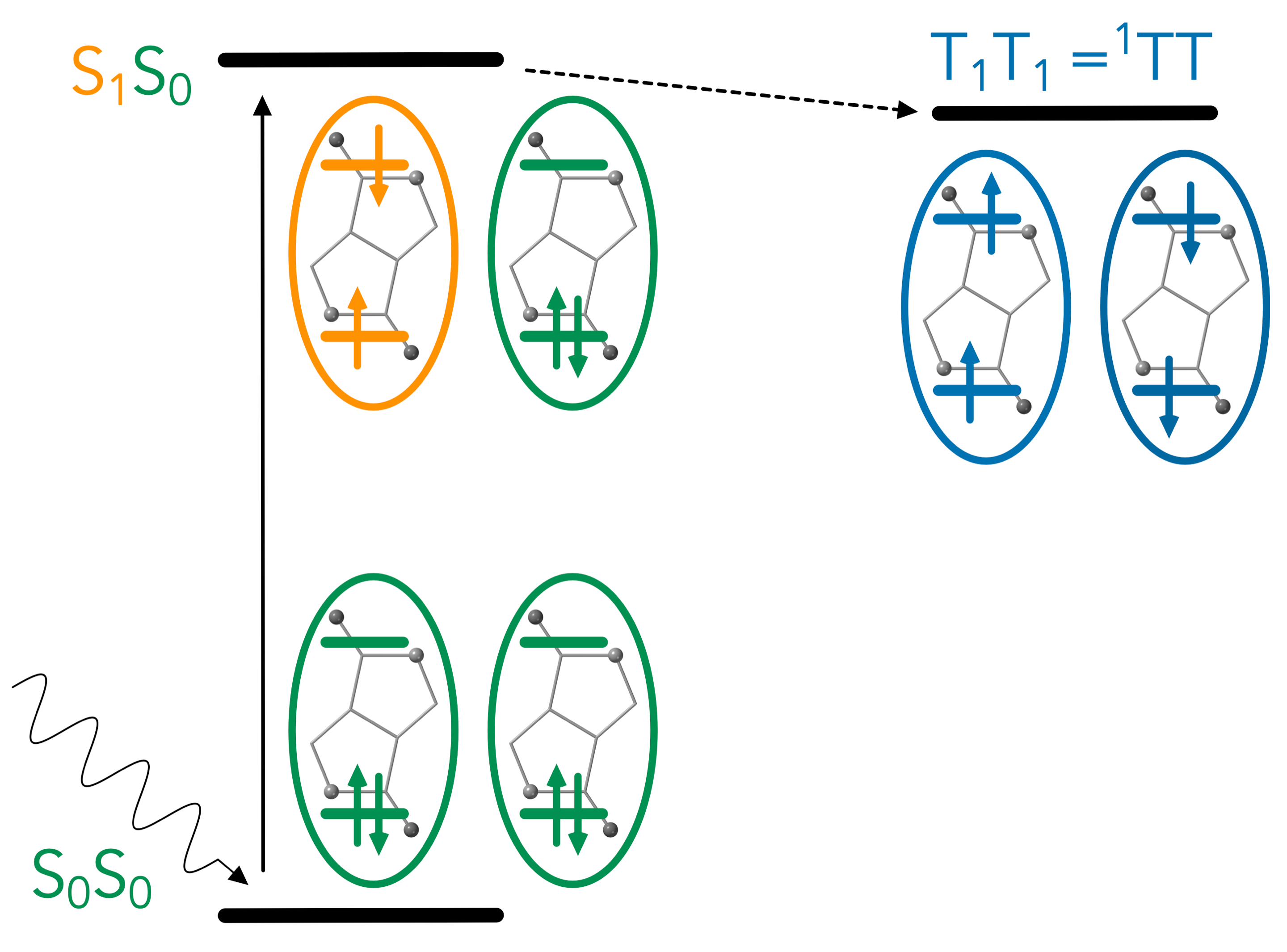
Figure 1

A second important part of this project is the continuous optimization of the efficiency of the GronOR code and the implementation of new features. As shown in Figure 2, the code scales linearly with the number of nodes on which it is executed and some test runs have shown that the calculation is about 20 times faster when GPU are used compared to a CPU-only run. However, further improvements would certainly widen the applications range of the NCOI approach and we are currently investigating how the Cholesky decomposition of the two-electron integrals can be implemented in the code. Furthermore, the code has to be extended with a property module and the calculation of (numerical) gradients should be automatized. This programming effort should lead to an even more powerful GronOR code.

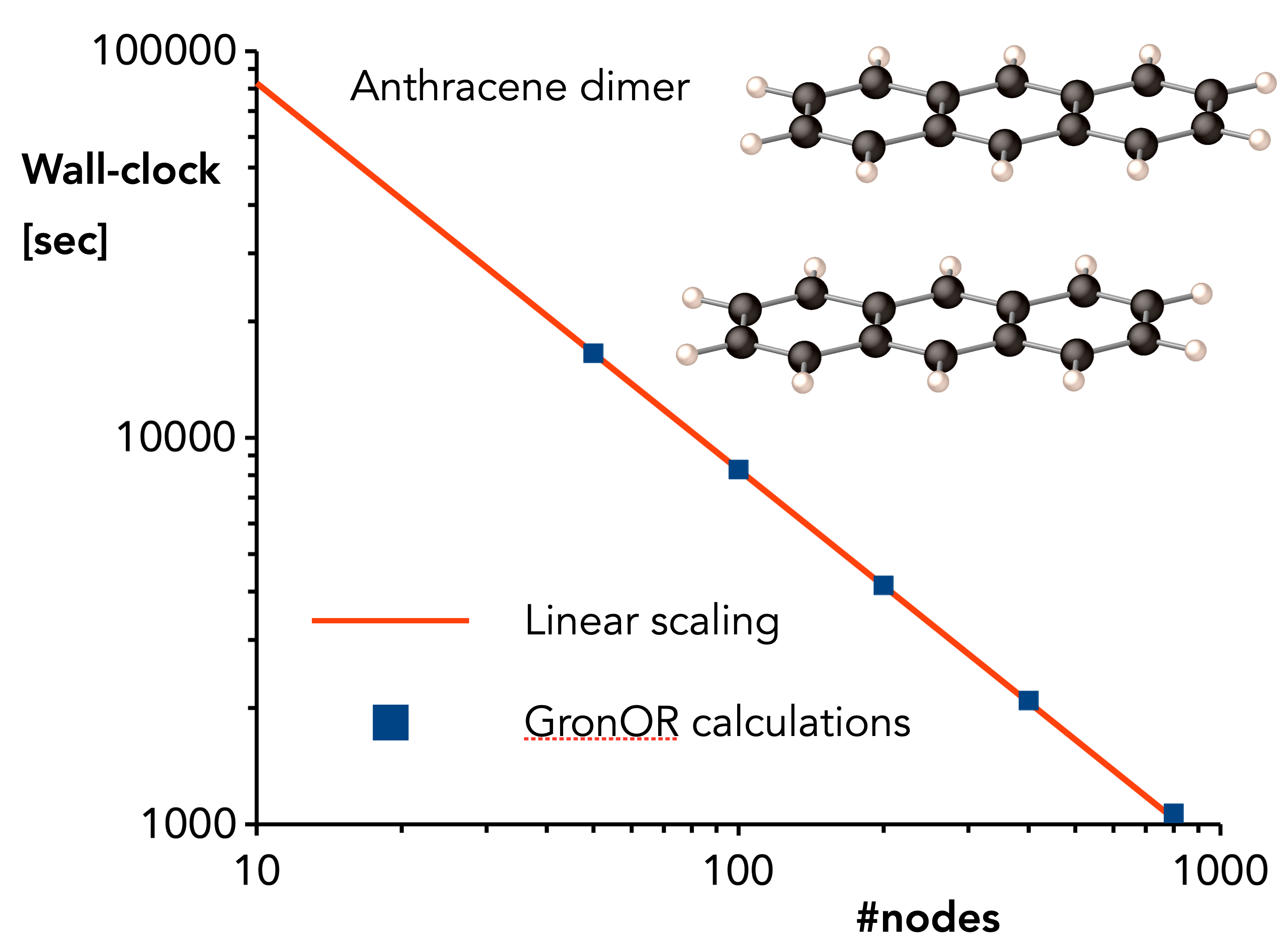
Figure 2

Relevant references:

www.gronor.org

gitlab.com/gronor

R. K. Kathir, C. de Graaf, R. Broer, and R. W. A. Havenith, Reduced Common Molecular Orbital Basis for Nonorthogonal Configuration Interaction, J. Chem. Theory Comput. 16, 2941-2951 (2020).

T. P. Straatsma, R. Broer, S. Faraji, R. W. A. Havenith, L. E. Aguilar Suarez, R. K. Kathir, M. Wibowo, and C. de Graaf, GronOR: Massively Parallel and GPU-Accelerated Non-Orthogonal Configuration Interaction for Large Molecular Systems, J. Chem. Phys. 152, 064 111 (2020).